Excursions in Math Chapter 19: Symmetry and Patterns
A Rigid motion (or isometry) is a motion applied to an object which do not change the size or shape of the object.
There are four types of rigid motions in a two dimensional plane.
Reflection across a line
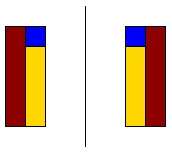
Here the object on the right is obtained from the object on the right by reflecting the object across the line.
Changing the line you reflect about will give a different reflection.
Rotation about a point
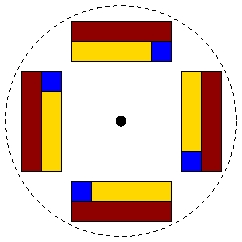
Here the object on top is rotated 90 degrees about the point to get the object on the right. The other images are rotations of 180 degrees and 270 degrees. The corners of the red rectangle follow the path of the dotted circle for rotations about the point, and rotations of amounts other than 90, 180, or 270 degrees are possible.
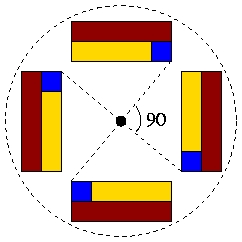
Changing the point you rotate about can give a different rotation.
Translation in a particular direction
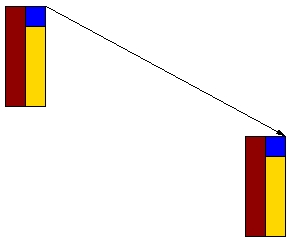
Here the object is translated a certain distance in a particular direction.
Glide reflection across a line
Glide reflection is the combination of a reflection and translation. In glide reflection, each successive element in the design in a reflection of the previous one.
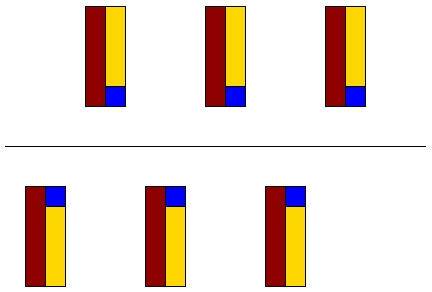
The second element (the first one above the line) is found from the first element (first one below the line) by reflecting about the line and translating to the right. This process is repeated to come up with the final design.
Any rigid motion in the plane is made up of combinations of these four motions.
Symmetry means that an object looks the same when a transformation is applied. Whether or not an object has a symmetry depends on what line you reflect about, or what point you rotate about, or what direction you translate in. ``Looks the same'' means indistinguishable from itself, so if the object has moved to a different location, we can see that and there will be no symmetry.
So when we talk about symmetry of an object, we have to include the details of how we are doing the reflection, rotation, or translation. We speak of things like ``symmetric with respect to reflection about the diagonal''.
Example: What kinds of symmetry does the following object have?
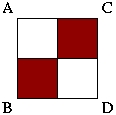
I have labelled the corners of the object with letters so we can track how it moves. The letters can move to different places, but the object must still look the same for it to have a symmetry.
Stay Put: It may seem strange to single out Stay Put as a transformation, since the object is not being changed at all. But it is an important thing that mathematicians do. Examples of Staying Put are adding zero when doing addition, or multiplying by one when doing multiplication, since in both cases the number doesn't change. For rigid motions, Stay Put means do not change the orientation of the object in any way, so the labels on the corners remain the same.

Reflection: There are only two lines which we can reflect about and the object will still look the same.
The first reflection symmetry is a line joining corners B and C.

Notice how the shape looks the same after the reflection--we could not tell that a reflection had been performed except that the labelling of the corners has changed. This change in the labels is what allows us to track the rigid motion.
The second reflection symmetry is a line joining corners A and D.

These two reflection symmetries all the only reflection symmetries of the object.
Rotation: You can rotate by different amounts, and around different points. We need to rotate about the center of the object, since if we rotate about a different point we will be able to tell that the object has moved (it is in a different position). This object has a half turn (or 180 degrees) rotation symmetry about its center.

You could also do a full turn rotation, but that would put the corner labels back in their original positions, so it would be like we had done nothing to the object. This is just the Stay Put operation we saw before.
Translation: No. Since the object is no longer in the same location as it started in, there is no translation symmetry. We can perceive that the object has been moved.
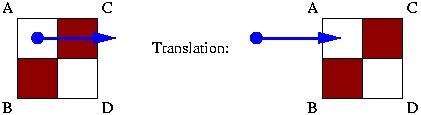
Glide Translation: No. Since the object does not have translational symmetry, it does not possess glide translational symmetry.
We have seen that our object has four symmetry transformations:
- The Stay Put transformation. We can call this symmetry operation E.
- Reflection about a line joining corners B and C. We can call this symmetry operation A.
- Reflection about a line joining corners A and D. We can call this symmetry operation B.
- Rotation by a half turn about the center. We can call this symmetry operation C.
The set of these operations {E,A,B,C} is called a group. A group is a mathematical concept that involves elements from a set that behave in certain ways. Not all lists of operations of groups, but this one happens to be a group.
A pattern in art will only have finitely many repetitions of an object (think of wallpaper, for example, which repeats itself) but we could think of the pattern as extending indefinitely for mathematical purposes.
The symmetries of the pattern are the set of rigid motions which preserve the pattern (all the parts of the pattern appear in the same places once the rigid motion has been applied). It is like if we looked at the pattern, turned out back and someone moved the object somehow, and when we looked at it again we couldn't tell that it had been moved.
Patterns can be classified into three types. If the pattern has infinitely many repetitions in:
no direction it is a rosette pattern (example: How to Make Paper Rosettes), 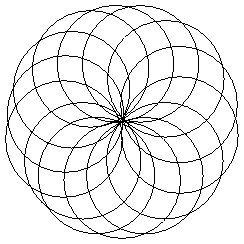
Rosette patterns appear in flowers, and anything where a circular repetition is seen. A rosette pattern may or may not have reflection symmetry.
one direction it is a strip pattern (example: Hairpin Lace Strip Tutorial 20 Triangle Elements In The Middle) 
Strip patterns appear in many kinds of art, and anything with a linear translation of a motif. A strip pattern has horizontal translation symmetry, if the length of the horizontal translation makes the pattern match up.
two directions it is a wallpaper pattern, 